یافتن پاسخ برای یک مسئلهی ریاضی که معمولاً حلنشدنی تلقی میشود، میتواند تمام اعتماد موجود در اینترنت را زیر سؤال ببرد. آیا واقعاً این کار عملی است؟ تمامی کارشناسان رایانه امیدوارند که اینطور نباشد!
رمزنگاری نامتقارن که امنیت در اینترنت بر اساس آن بنا شده متکی به یکی از دو فرضیات ریاضی است؛ این فرض میگوید که، بجز روش جستجوی فراگیر، تعیین عوامل اعداد صحیح بزرگ زمانی که این عوامل دو یا چند عدد اول بزرگ باشند، غیرممکن است یا پیدا کردن لگاریتم گسستهی یک عنصر تصادفی منحنی بیضوی با توجه به یک نقطهی پایهی عمومیِ شناخته شده غیرعملی است.
«جستجوی فراگیر یا Brute Force» در این مورد یعنی باید تمامی احتمالات را بررسی کنید تا موردی را پیدا کنید که جواب دهد. در یک الگوریتم جدید معمولاً تعداد احتمالات خیلی زیاد است و این امر حتی با وجود منابع محاسباتی گسترده نیز بسیار بسیار زمانبر خواهد بود.
اما اگر زمانی این فرضیات دیگر معتبر نباشد چه میشود؟ اگر به هر دلیلی فاکتورگیری (تجزیه به عوامل اول) اعداد اول بزرگ و یا تعیین لگاریتم گسستهی یک عنصر تصادفی منحنی بیضوی با منابع محاسباتی معقول انجامشدنی باشد، چه میشود؟
اگر این امر شدنی باشد امنیت بخش عمدهای از اینترنت و حتی محاسبات غیراینترنتی بلااستفاده میشود.
بروس اشنایدر، کارشناس رمزنگاری، در مقالهی اخیر خود با عنوان «The Cryptopocalypse» پاسخی به یکی از بخشهای کنفرانس بلکهت داد. اشنایدر چندان نگران نیست و دلایل او به نظر قانعکننده میآید. وی توضیح داد که هر چه پیش میرویم فاکتورگیری آسانتر میشود؛ آسانتر از آن که فکرش را بکنید و در ادامه چهار دلیل برای گفتهی خود ذکر کرد:
- رایانهها سریعتر شدهاند.
- رایانهها بهتر شبکه میشوند.
- الگوریتمهای فاکتورگیری کاراتر شدهاند.
- پیشرفتهای اساسی در ریاضیات الگوریتمهای فاکتورگیری بهتری را در اختیار ما قرار میدهد.
وی اضافه کرد که این مسأله بسیار شبیه به مسألهی لگاریتم گسسته است. درواقع رایانهها همواره در حال سریعتر شدن هستند و شبکهها نیز رایجتر و پرسرعتتر میشوند. این بدان معنی است که اختصاص منابع محاسباتی گسترده به مسائلی چون شکستن کلید با جستسجوی فراگیر آسانتر میشود.
این اتفاق به واقع میتواند زیرساخت کلید عمومی (Public_key_infrastructure) را منسوخ کند. با وجود آن که 3 دلیل دیگر شکستن کلیدها را ممکن میسازد اما در این بین استانداردها نیز در حال پیشرفت هستند و کلیدها را بزرگتر ساخته و در نتیجه شکستن آنها را سختتر میکنند. کنفرانس بلکهتی که اشنایدر به آن اشاره داشت بیان کرده بود که این مسابقه کلیدهای RSA را مجبور میسازد که از عبارات بسیار بزرگ غیرقابل کنترل استفاده کنند؛ اما ECC به عنوان یک راه گریزی باقیمانده چرا که به کلیدهای کوچکتری نیاز دارد و شکستن آن نیز زمان کمتری را طلب میکند.
رمزنگاری منحنی بیضوی (ECC یا Elliptic curve cryptography) یک رمزنگاری به روش کلید عمومی میباشد که بر اساس ساختاری جبری از منحنیهای بیضوی بر روی زمینههای محدود طراحی شده است. استفاده از منحنیهای بیضوی در رمزنگاری به طور جداگانه توسط نیل کوبلیتز و ویکتور س. میلر در سال 1985 پیشنهاد شد. منحنیهای بیضوی همچنین در چندین الگوریتم فاکتورگیری عدد صحیح نیز استفاده شدهاست که این الگوریتمها دارای کاربردهایی در زمینهی رمزنگاری میباشند، مانند فاکتور منحنی بیضوی Lenstra.
درست است که تغییر بستر و نرمافزار موجود مستلزم تحمل هزینه و مسئولیت زیادی است و به همین دلیل هنوز بسیاری از شرکتها از الگوریتمهای رمزنگاری منسوخ و قدیمی استفاده میکنند اما به هر حال گزینههای رمزنگاری قوی و جدیدی نیز برای کسانی که مایل به سرمایهگذاری در آنها هستند، وجود دارد. اگر فرضیات اساسی ریاضی پشت این روشها از بین رفته و نقض شود، دیگر امنیتی وجود نخواهد داشت و در آن صورت دیگر مهم نیست که چقدر در این شیوهها سرمایهگذاری شده است.
البته اشنایدر در این باره نگران نیست. وی مفهوم عملکرد اخیر ریاضی را که گفته میشد مسئلهی لگاریتم گسسته را حل میکند انکار کرد و گفت هیچ عملکرد ریاضی نمیتواند فرضیات مهم را زیرسوال ببرد.
البته این حرف تنها کمی از شدت ترسناکی ماجرا میکاهد. پیشرفت در شکستن رمزنگاری منحنی بیضوی ممکن است از جهتی اتفاق بیفتد که اشنایدر از آن مطلع نیست. حتی ممکن است چنین تکنیکی را در ازای دریافت پول زیاد به فروش برسانند. با وجود این در چنین شرایطی امکانی برای دفاع از خود باقی نمیماند. بنابراین میتوان اینطور فکر کرد که تقریباً تمامی اعتماد موجود در دنیای اینترنت مبتنی بر یک مسئلهی ریاضی خاص است که شاید زمانی بیابد که این وابستگی را نوعی حماقت بدانیم.
دربارهی رمزنگاری کلید عمومی بیشتر بدانید:
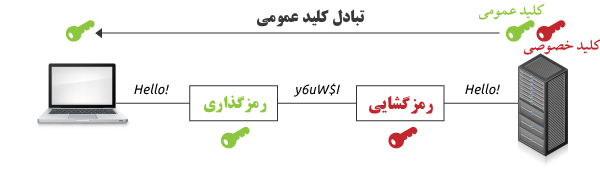
رمزنگاری کلید عمومی یا رمزنگاری نامتقارن (Public Key Cryptography or asymmetric cryptography) روشی از رمزنگاری است که کلید مورد استفاده برای رمزگذاری با کلید مربوط برای رمزگشایی با هم متفاوت است (برخلاف رمزنگاری متقارن که در آن رمزگذاری و رمزگشایی با یک کلید انجام میشود). با کلید مخصوص رمزنگاری نمیتوان رمزگشایی پیام را انجام داد و آن کلید فقط برای رمزنگاری بکار میرود و افشا شدن آن هم لطمهای به کسی نمیزند؛ بدان جهت که با آن کلید نمیتوان متون رمز شده را برگرداند و پیداکردن کلید رمزگشایی از روی کلید رمزنگاری نیز کار سادهای نیست. در رمزنگاری نامتقارن، کاربر یک جفت کلید در اختیار دارد:
- کلید عمومی (برای رمزگذاری متن اصلی و بررسی صحت امضای دیجیتال)
- کلید خصوصی (برای رمزگشایی متن رمز و امضای دیجیتال دادهها)
مشخص است که کلید خصوصی باید مخفی باقی باشد؛ ولی کلید عمومی را میتوان به طور وسیع منتشر کرد. پیامهای دریافتی کد شده توسط کلید عمومی کاربر فقط برای خودش قابل خواندن است؛ زیرا تنها خودِ کاربر است که کلید خصوصی وابسته به کلید عمومیِ خود را جهت رمزگشایی در اختیار دارد.
اما این دو کلید با هم رابطهای ریاضی دارند ولی عملاً گفته شده که کلید خصوصی از روی کلید عمومی قابل محاسبه نیست.
رمزنگاری کلید عمومی مبتنی بر اشکالات برخی از مسائل ریاضی است. در اوایل سیستمهای مبتنی بر کلید عمومی با این فرض که پیدا کردن دو یا بیشتر از دو عامل اول بزرگ برای یک عدد صحیح بزرگ مشکل است امن تلقی میشدند. برای پروتکلهای مبتنی بر منحنی بیضوی، فرض بر این است که پیدا کردن لگاریتم گسسته از یک عنصر تصادفی منحنی بیضوی با توجه به یک نقطه پایهی عمومیِ شناخته شده غیرعملی میباشد. اندازه منحنی بیضوی تعیین کننده سختی مسئلهاست. مزیت اصلی که توسط ECC وعده داده میشد یک کلید با اندازه کوچکتر بود، که این موضوع به معنی کاهش ذخیرهسازی و انتقال مورد نیاز است؛ به این معنی که یک سیستم منحنی بیضوی میتواند همان سطح از امنیت را که یک سیستم مبتنی بر RSA با مولفههای بزرگ و طول بلند کلید فراهم میکند، ایجاد کند. به عنوان مثال، یک کلید عمومی 256 بیتی مبتنی بر ECC میبایست امنیت قابل مقایسهای با یک کلید عمومی 3072 بیتی مبتنی بر RSA داشته باشد. برای اهداف امروزی رمزنگاری، منحنی بیضوی یک منحنی مسطح است که متشکل از نقاط رضایت بخش معادله میباشد.
y^2 = x^3 + ax +b
منبع: news.asis
گیگ بوی سایت آموزش شبکه به صورت فارسی و تصویری و دانلود نرم افزار